선형 칼만 필터란?
칼만 필터는 dynamic system 같은 확실한 정보가 있지 않은 곳에 사용될 수 있으며, 이 시스템이 다음에 수행할 task에 대해 추측을 할 수 있습니다. 그리고 칼만 필터는 센서를 통해 추측한 정보에 끼여있는 노이즈 제거에도 좋은 역할을 합니다. 이 필터에 이상적인 시스템은 매 시간 혹은 매 프레임마다 변화하는 시스템에 이상 적라고 생각합니다. 왜냐하면 어떤 시퀀스에 필요한 연산 작업에 많은 데이터양이 아닌 이전 데이터 이외의 데이터는 유지할 필요가 없기 때문입니다. 그렇기 때문에 비교적 빠른 연산 과정으로 실시간 문제 해결 및 저전력 PC, 임베디드 시스템에 적합합니다.
칼만 필터 적용 사례
칼만 필터에 대한 이야기를 시작하기 전에 간단하게 칼만 필터를 어떤 식으로 활용하는지에 대해 알아보겠습니다. 자율주행 로봇에 대한 예시를 들어보면, 현재 어떤 로봇에 대한 이동 명령을 내려 A지역에서 B지역으로 로봇을 이동시켜야하는 상황에서 로봇이 현재 어디에 있는지 정확하게 알아야 합니다. 그러면 로봇의 위치를 어떻게 나타낼 것인지에 대해 먼저 정의를 내려야 합니다. 우리는 로봇의 상태를 통해 로봇의 위치를 알아낼 수 있고, 로봇의 상태는 (로봇의 위치 정보, 로봇의 속도)입니다. 로봇의 위치 정보만으로 로봇의 정확한 위치를 표현할 수 있으면 좋지만...(위치 정보를 나타내는 센서의 경우 GPS 센서가 있습니다. 하지만, 이 센서의 정확도가 약 10m(오차율)라고 가정했을 때 만약 이 GPS 센서만을 사용하여 이동을 한다면 정확하게 위치를 추정하기는 어렵습니다.) 따라서 GPS 센서만으로 위치를 파악하는데 부족한 점이 많고 이런 점을 개선하기 위한 방법으로 로봇의 속도 또한 같이 사용하여 로봇의 위치를 예측해야 하는데 이를 칼만 필터를 통해 찾기도 합니다.
칼만 필터는 예측단계와 추정(업데이트) 두 개의 시퀀스를 가지는 필터입니다. 말로 풀어서 간단하게 설명하면,
1. 대충 이전의 데이터를 가지고 다음에 들어올 입력값을 미리 예상해 놓는다.(예측 단계)
1.2. 예측값의 분산 계산(공분산 계산단계)
2. 입력이 들어왔다(observation model).
3. 입력 데이터와 예측 데이터를 비교해서 최적의 출력 값을 추정(업데이트 단계).
위 시퀀스 1~3 단계를 이해하면 칼만 필터를 설명할 수 있습니다.
1. 대충 이전의 데이터를 가지고 다음에 들어올 입력값을 미리 예상해 놓는다. (예측 단계)
1-1. Space State Model(SSM)
아주 간단하게 로봇의 상태를 거리와 속도로 정의한다고 했을 때
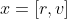
우리는 연속적인 세계에 살고 있지만, 디지털적인 세상에 사는 사람들을 위해 샘플링 속도를 dt라고 정의를 내렸을 때, 우리의 시스템 모델(시스템 매트릭스)은 아래와 같이 정의할 수 있습니다.

로봇의 상태 모델(k시간에서의 시스템의 상태)은 ((k-1) 우리의 시스템 모델 * 로봇의 상태)으로 표현할 수 있습니다.

1-2. Covariance matrix
어떤 정밀한 센서 혹은 계산 과정에서 측정/예측에 대한 결과 값은 반드시 오차를 가져옵니다. 우리는 True Value(진치)를 알 수 없고, 불확실한 측정에 의해서 나온 데이터로 추정할 수밖에 없기 때문입니다. 즉 매 순간 노이즈가 발생한다는 것을 알고 있어야 합니다.
- Process noise covariance [Q]
- Measurement noise covariance [R] (측정 후 노이즈)
- State covariance [P]
Process noise covariance


[Q]는 일반적으로 0에 근사하다고 알려져 있지만, 사실 Q의 값을 선택하는 과정에서는 고려해야 하는 몇 가지 사항들이 있습니다. 하지만 보통 process noise covariance의 평균은 0에 근사하다 라고 하며 이를 white noise라고 말합니다. (시스템 노이즈)
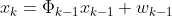
measurement noise covariance
측정 후 데이터에 대한 노이즈는 예를 들어 거리와 속도 두 가지로 생각했을 때, 우리가 생각한 거리의 결과와 실제 결과의 차이가 0.03cm이고 , 생각한 속도의 결과와 실제 속도의 차이가 0.2m/s 일 때 이 두 개의 시그마(분산)로 measurement noise convariance를 만들어 측정 후 노이즈를 구할 수 있습니다. 즉, 이 measurement noise covariance의 역할은 얼마나 측정값에 노이즈가 끼였는지를 나타내는 지표지입니다.

State (co) variance
State covariance 혹은 error covariance라고도 합니다. 결국 우리는 error covariance가 최소화되도록 우리들의 추정치와 예측치를 사용하여 최적의 추정치를 찾아야 하는 게 궁극적 목표입니다. 상태 공분산(state covariance)은 크게 두 가지로 구별할 수 있는데 관측 모델 전, 후로 나뉠 수 있습니다. 표기는 아래와 같이 사용합니다.
오차 공분산의 예측값 (Observation model X)

오차 공분산의 예측값 (Observation model O)
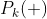
관측 전 로봇의 상태 모델 추정 값
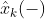
관측 후 로봇의 상태 모델 추정 값
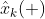
먼저 관측 모델 전 오차 공분산의 예측값을 구하려면 아래와 같이 구할 수 있습니다.
1. 오차에 대한 정의는 아래와 같습니다.

위 오차에 대한 정의를 사용하면 관측 전 예측 오차에 대한 정의는 아래와 같습니다.

2. 분산 값에 대한 정의는 아래와 같습니다.
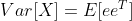
찬찬히 식을 뜯어서 보면 E 기댓값 안에 있는 e 오차들은 1. 관측 전 예측 오차에 대한 정의로 치환을 할 수 있습니다. 그러면 예측 공분산 식은 아래와 같이 만들 수 있습니다.

그리고 치환한 예측 오차들을 풀어주면 아래와 같은 예측 공분산 식을 나타낼 수 있는데,
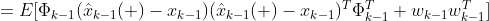
예측 공분산 안에 있는 수식을 천천히 살펴보면 우리가 바로 위에서 구한 2. 예측 공분산 P_k에 대한 식을 볼 수 있습니다. 이 식의 가운데 부분이 결국 P_k-1로 치완하면 아래와 같이 관측 전 오차 공분산의 예측값을 구할 수 있습니다.
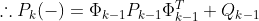
2. 입력이 들어왔다(observation model).
이제 관측 후에 오차 공분산의 예측값을 구하려면, 먼저 관측 모델(observation model)에 대한 정의를 내려야 합니다. 관측 모델은 아래와 같이 H로 대칭 행렬로 표현할 수 있는데 아래 값은 예시일 뿐 공간 상의 벡터 크기나 상황에 따라 언제든지 바뀔 수 있습니다.

이후에 관측 모델을 통하여 관측치를 (측정) 만들어 낼 수 있고 관측치와 칼만 게인이라는 변수를 사용하여 모델이 관측되고 난 후에 오차 공분산의 예측값을 구할 수 있습니다.
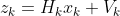
관측치 = (관측 모델 x 로봇의 상태 모델) + measurement noise
3. 입력 데이터와 예측 데이터를 비교해서 최적의 출력 값을 추정(업데이트 단계).
칼만 추정식이 아래와 같이 정의된다고 했을 때,
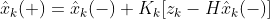
칼만 추정식은 알파 베타 함수의 한 종류인, 지수 이동평균 필터를 기반으로 만들어졌습니다.
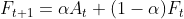
여기서 A는 실측치, F는 필터링 후의 값이고, 간단하게 생각하면 알파 + 베타 = 1 이 나오게 설정이 되어 있는 필터 디자인 모습이라고 보면 됩니다. 이제 위에서 정의한 칼만 추정식을 풀어서 보면 H 관측 모델을 1로 치완하고 알파 베타 형태로 바꾸면 아래와 같이 나타 낼 수 있습니다.
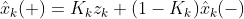
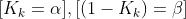
알파베타 함수는 알파+베타의 합이 1이 나오게 설정되어 있는 필터이기 때문에 즉, 칼만 게인이 크게 나오면 측정치 z_k를 더 신뢰하고, 칼만게인이 작게 나오면 예측치 x_k(-)를 더 신뢰한다는 의미가 됩니다.
그렇다면 이제 칼만 게인을 구하는 방법을 알아야 하는데... 칼만 추정식에 관측치 z_k를 대입하면 아래와 같이 관측 후 로봇의 상태 모델 추정 식을 나타 낼 수 있습니다.

1. 오차에 대한 정의는 아래와 같습니다.

위 오차에 대한 정의를 사용하면 관측 후 예측 오차에 대한 정의는 아래와 같이 나타 낼 수 있습니다.
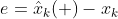
2. 분산 값에 대한 정의는 아래와 같습니다.
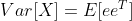
찬찬히 식을 뜯어서 보면 E 기댓값 안에 있는 e 오차들은 1. 관측 후 예측 오차에 대한 정의로 치환을 할 수 있습니다. 그러면 예측 공분산 식은 아래와 같이 만들 수 있습니다.

관측 후 예측 공분산 식을 차례대로 전개하면 아래와 같이 식이 나열이 되는데
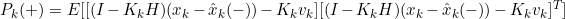
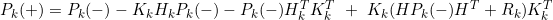
결국 추정치 공분산에 대한 값을 가장 작게 만들기 위해 위 식을 시간 t에 대해 미분을 하게 될 때

미분 값을 최소가 되게 하는 칼만 게인 K_k를 구하면 됩니다.
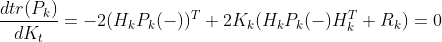
칼만 게인을 구하기 위해 K_k를 제외한 모든 값들을 왼쪽으로 이항 시키고
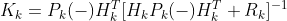

관측 모델 H를 1로 치환하여 간단하게 하면 아래와 같이 칼만 게인에 대한 식을 구할 수 있습니다.

알고리즘 정리

칼만 필터 알고리즘은 아래 2가지 조건이 성립이 돼야 사용할 수 있습니다.
1. 모션 모델과 측정 모델이 linear 한 경우
2. 모션 모델과 측정 모델이 gaussian 분포를 따를 경우
선형 칼만 필터는 상태 예측과 측정 업데이트를 반복적으로 수행하며 로봇의 현재 위치를 계산합니다. 하지만 칼만 필터를 사용할 때 제일 중요한 것은 시스템 모델입니다. 시스템 모델이 실제 시스템과 최대한 비슷해야 최고의 효과를 얻을 수 있습니다.
시스템 모델은 칼만 필터를 사용해서 칼만 게인처럼 변화하는 값이 아니라 동작 전에 미리 설정해놓는 고정적인 값이므로 얼마나 최적의 시스템 설계를 설정했냐에 따라 칼만 필터의 성능이 달라집니다.
마지막으로 선형 칼만 필터는 위 두 가지 경우가 갖춰지는 경우에만 사용할 수 있는 단점이 있습니다. 하지만 대부분의 실제 시스템은 가우시안 분포를 따르지 않으며 비선형 모델을 포함합니다. 이러한 문제점을 해결하기 위해 확장형 칼만 필터가 나오기도 했습니다.
'Machine learning' 카테고리의 다른 글
| Linear Regression (0) | 2021.09.22 |
|---|---|
| Random Forest (0) | 2021.09.20 |
| Decision Tree (0) | 2021.09.19 |
| correlation coefficient (피어슨 상관계수) (0) | 2021.08.24 |
| covariance matrix (공분산 행렬) (0) | 2021.08.21 |