Regression?
Supervised learning은 레이블링 된 Training data를 학습하여 하나의 모델(함수)을 만들고, 이후에 만들어진 모델에 레이블링 되지 않는 Test data를 집어넣어 입력된 data에 대한 맞는 답을 찾는 과정을 말합니다.
이때 레이블링 된 답이 어떤 형태인지에 따라 모델은 분류 또는 회귀 과정을 통하여 답을 예측합니다. 예를들어 아래의 그림과 레이블링 된 값이 서로 딱딱 떨어지게 구분되는 경우는 입력 데이터가 A냐 B냐 C냐 완벽하게 서로 완벽하게 구분하면 이것을 '범주형 데이터'라 말하고, 레이블링이 범주형 데이터로 이루어진 학습 모델의 경우 각각의 값을 구별해내는 분류(Classification)를 이룹니다.

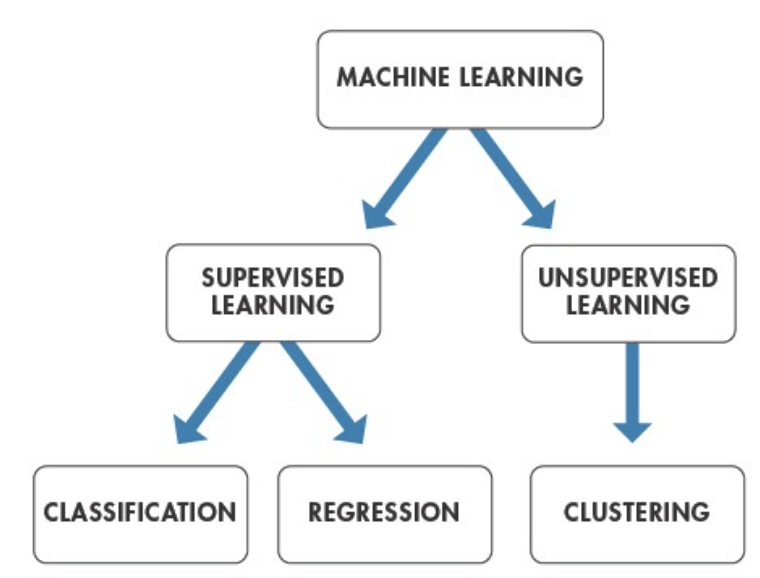
반면에 사람의 키와 몸무게에 대해 어떠한 범위 내에서 수치적인 형태로 존재할 경우 이를 '연속형 데이터'라고 하며, 레이블링 된 값이 연속형 데이터일 경우 입력 값과 출력 값 간의 일반적인 관계 특성을 도출하는 회귀(Regression)의 역할을 수행합니다.
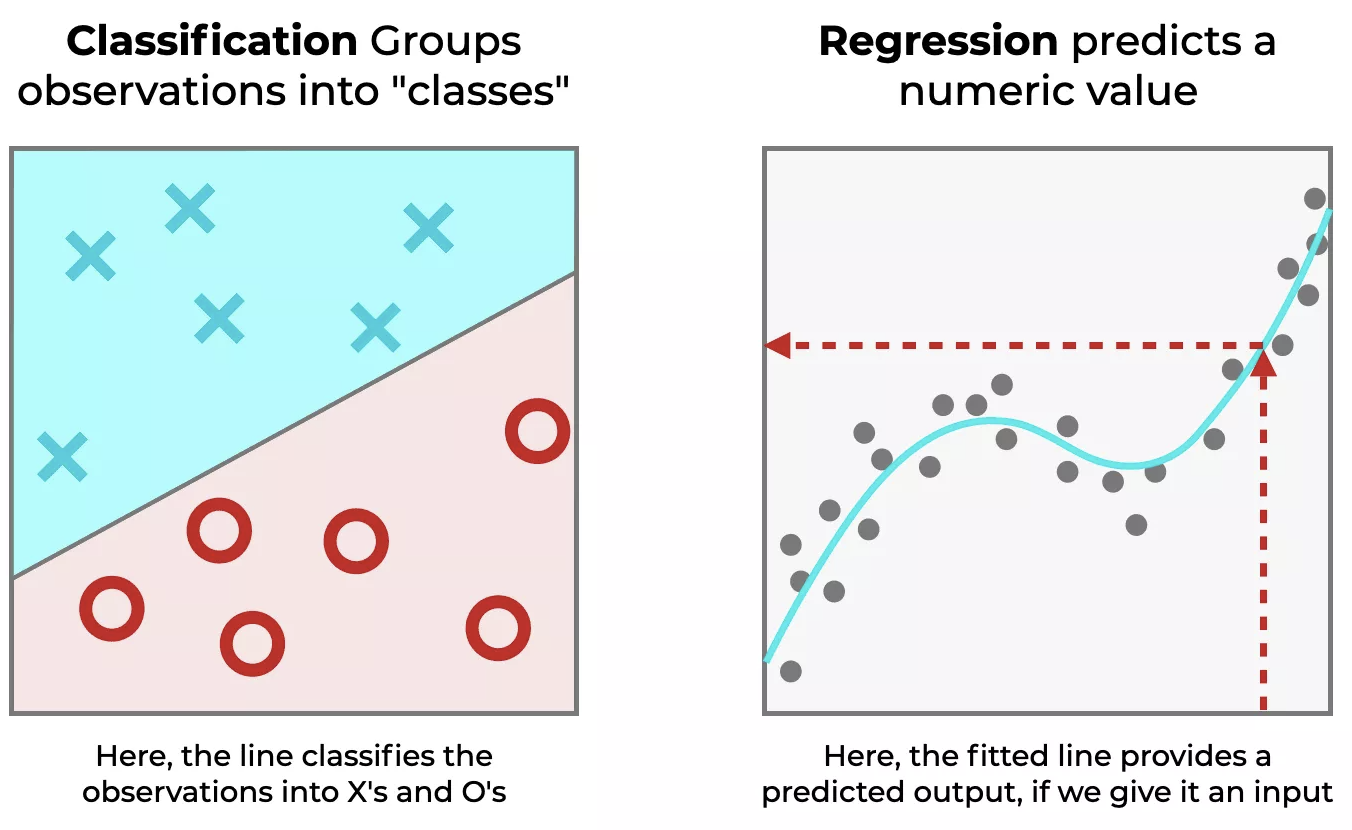
위 예시에서 왼쪽은 분류(classification)를 수행한 것이고 오른쪽은 회귀(regression)를 수행한 것입니다. 분류에서는 찾아야 할 값에 대해 명확하게 X냐 혹은 O냐에 대한 명확하게 구분을 할 수 있고, 회귀에서는 입력 데이터가 학습 모델에 따라 맞는 출력 데이터를 알 수 있습니다. 하지만 이 출력 데이터들은 모두 무작위 값들이 아니라 어떤 경향을 가지면서 분포한다는 것을 그래프를 통해서 알 수 있습니다.
이때 우리는 위 그림에서의 오른쪽 그래프처럼 적절하게 기울기를 조절해서 Training 데이터에 맞게 구성을 해야 하는 것이 목표입니다. 선형 회귀는 비교적 간단하면서도 많이 쓰이는 알고리즘입니다. 의미가 굉장히 직관적인데 임의의 분포한 데이터들을 하나의 직선으로 일반화를 시키는 것입니다. 물론 데이터의 갯수에 따라 (2차 함수 - 직선), (3차 함수 - plane), (n차함수 - hyper plane)로 일반화를 시켜야 합니다.
간단하게 2차함수로 구성된 예시를 들어보겠습니다.
요즘 서울 집 값이 폭등하고 있는데 넓은 집으로 이사 가고 싶은 게 저의 꿈입니다. 하지만 집의 크기가 넓어질수록 집의 가격도 그만큼 올라가겠지요. 왕십리역 부근 부동산을 돌아보니 대략적으로 집 크기에 맞는 집 가격들을 알아낼 수 있었습니다.
| 관측치 | 집크기(X)(단위: 평수) | 집가격(Y) (단위: 억) |
| 1 | 13 | 7.6 |
| 2 | 31 | 21.6 |
| 3 | 35 | 23.8 |
| 4 | 11 | 6.9 |
| 5 | 10 | 5.0 |
| 6 | 17 | 11.9 |
| 7 | 45 | 46 |
제가 알아낸 데이터(Training data)에 대한 모델을 만들어보면 아래와 같이 구성됩니다.

굉장히 깔끔한 직선이 만들어지는데 이제부터 제가 원하는 평수에 맞는 금액을 알아보면 37평이라는 X 입력 데이터를 넣어 Y 출력 데이터(집 가격)를 예측할 수 있습니다. (이제부터 우리는 입력데이터를 Input feature 출력 데이터를 Target variable이라고 칭하겠습니다.)
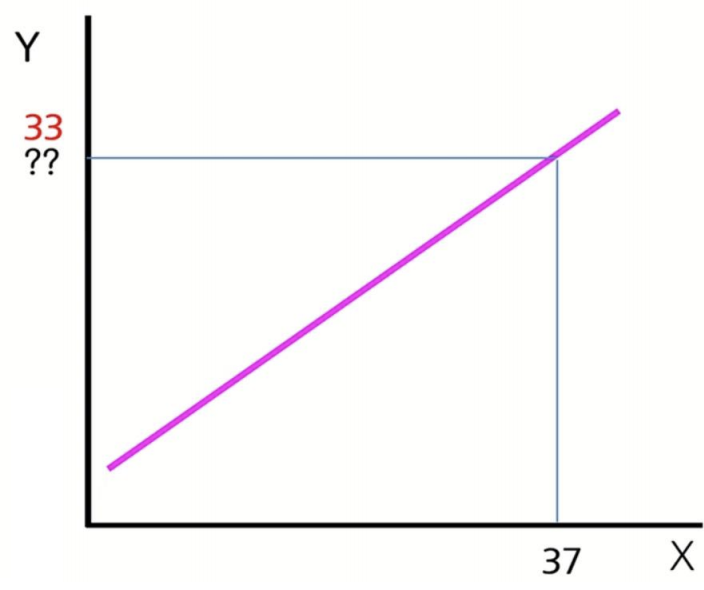
방금 전까지의 예시는 input feature가 한 개인 경우의 예시였지만 input feature가 많아지면 무수히 많은 차원이 만들어지겠지요. 이때 이것을 Multiple linear regression이라고 하고 single input feature만 있을 경우 simple linear regression이라고 합니다.
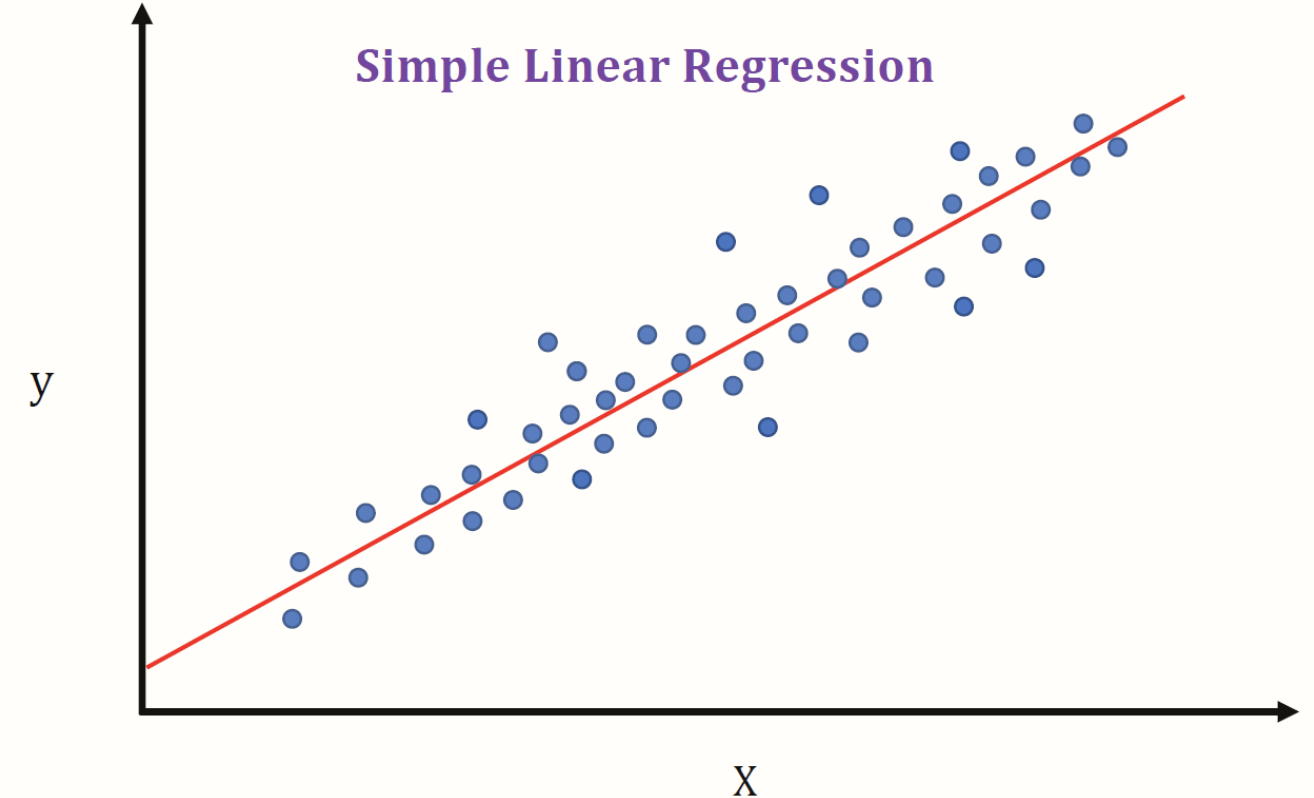

위 그림에서 Simple Linear Regression은 input feature가 1개인 반면에 Multiple Linear Regression는 input feature가 2개라 3차원 그래프가 구성됨을 볼 수 있습니다. 다시 한번 집고 넘어가면 우리가 regression에서 해야 하는 건 적절하게 그래프의 기울기를 조절해서 Training 데이터에 맞게 구성을 해야 하는 것이 목표입니다.
그렇다면 이 그래프의 기울기를 어떻게 Optimal하게 만드냐? 에 대한 문제를 해결해야 합니다.
How to solve the optimization problem?
먼저 Target data에 대한 cost function을 구성해야 하는데, 결국 이 cost function(혹은 loss function 혹은 error function이라고 부름)을 만들 때 사용한 Training data Y와 Test data Y의 error를 최소화를 시키는 cost function이 우리가 찾아야할 최적화 모델입니다. 그렇다면 이제부터 cost function을 구성하는 법을 보겠습니다.
1. Define a cost function E

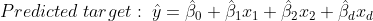
Training data y를 알고있을때 Test data y의 error차이를 최소화시켜주는 베타를 찾으면 가장 optimal 한 cost function입니다.
2. Getting optimal beta that minimizes E

error 최소화를 구하는 식에서 제곱을 해주는 이유는 test data나 training data의 값의 차가 음수가 나와 양수가 나온 다른 데이터들과 평등하게 비교해주기 위해서입니다.
만약 위에서 구한 cost function의 형태가 simple model일 경우 error가 최소화 시키는 베타를 미분을 통하여 구할 수 있습니다.
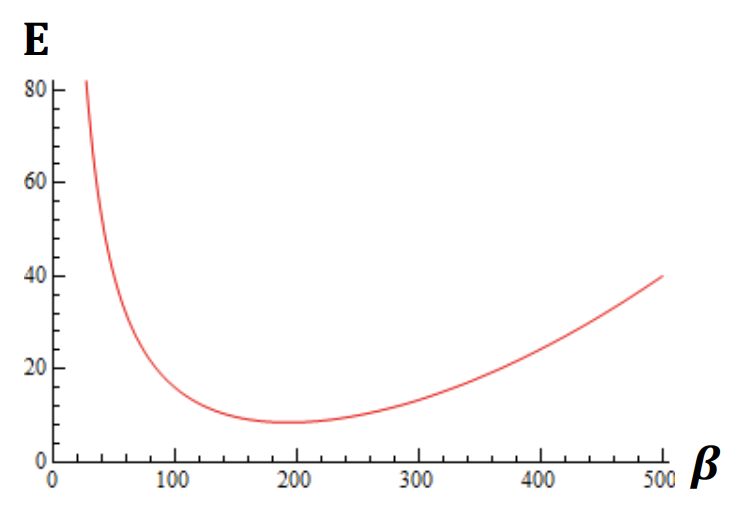



하지만 위와 같이 심플한 cost function이 아니라 굉장히 복잡한 function일 경우에는 미분을 통해서는 찾기 어렵습니다. 복잡한 function에 대한 error를 최소화시키는 방법은 다음 포스팅 때 올리도록 하겠습니다. 방금 전까지 우리는 error를 최소화시키는 cost function을 만들었습니다. 하지만 너무 training data에 과도하게 집착해버리면 Overfitting이 발생하게 됩니다.
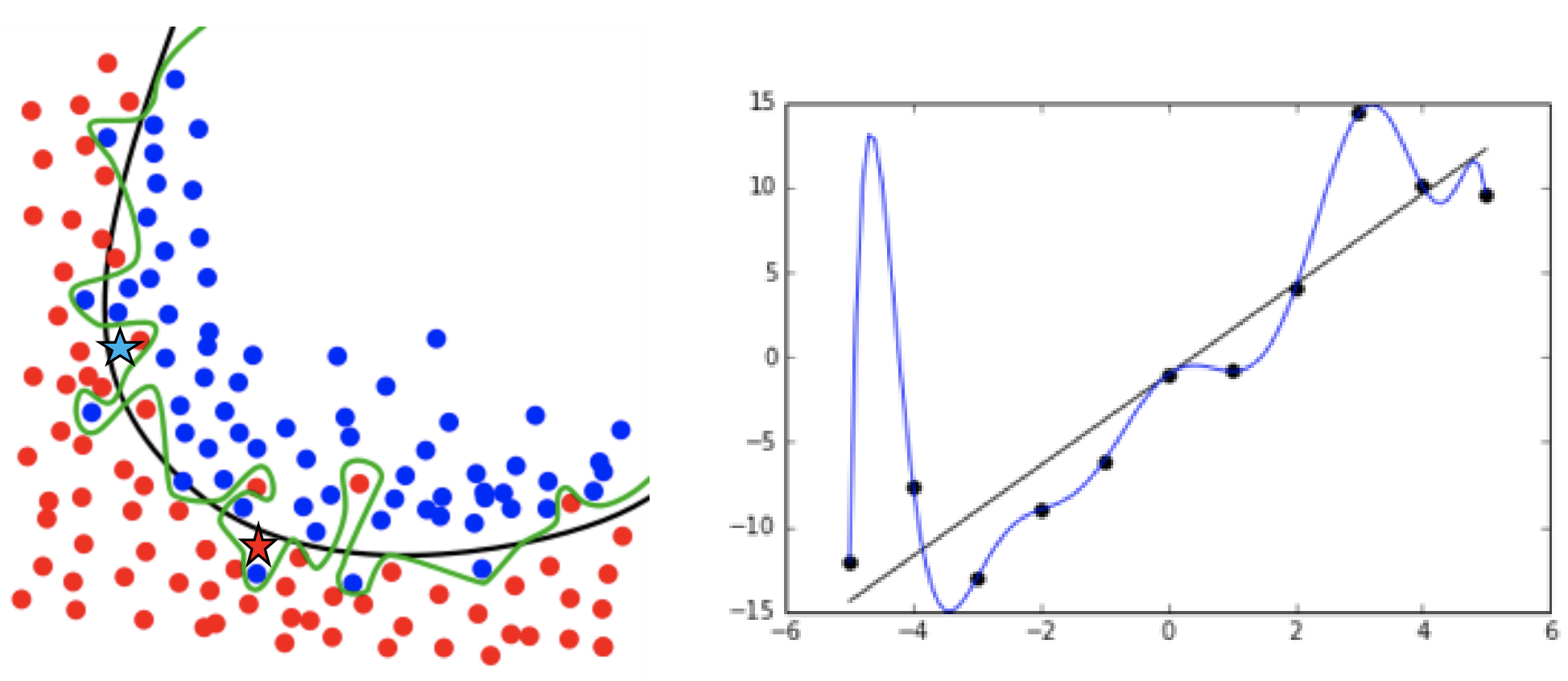
세개의 다른 모델 기반의 그림이 있습니다. training data는 모두 동일하다고 가정해봅시다.
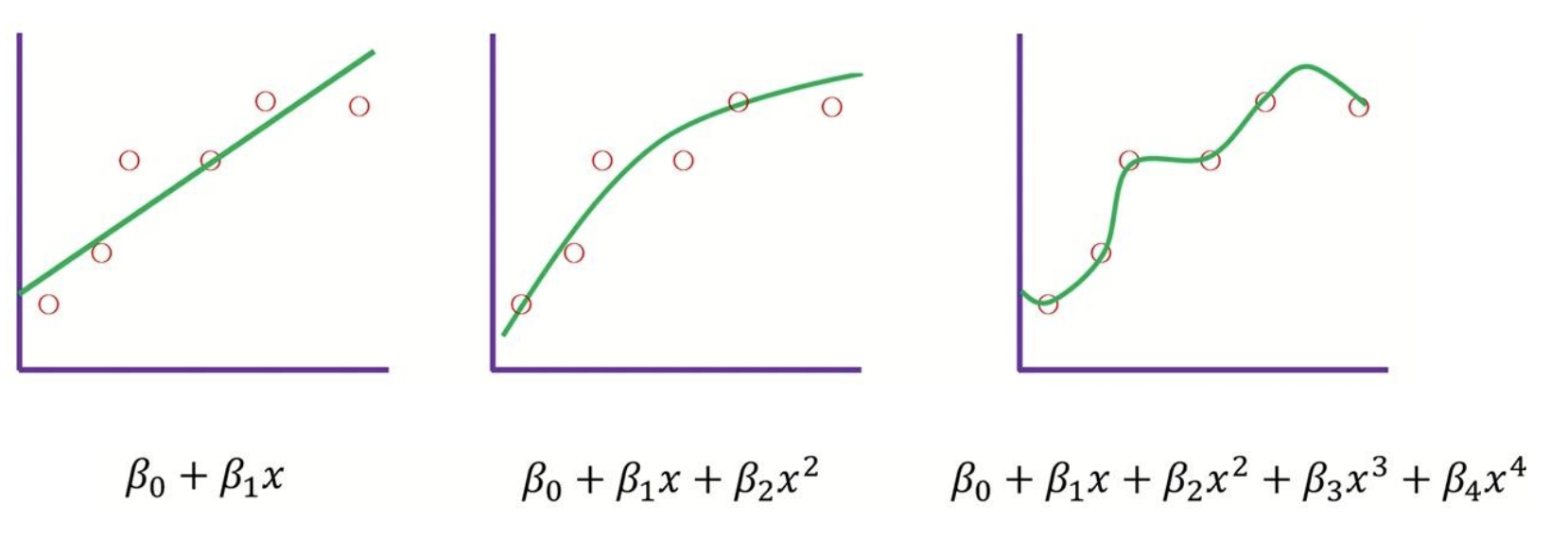
모두 training data에 맞게 작동은 잘하지만 test data에 대해서는 그나마 좋은 결과를 내는 모델이 무엇일까요? 확실한 건 우선 4차원 모델식은 training data에 대해서는 완벽한 성능을 낼 것 같지만 test data에서는 error가 많을 수도 있겠네요. 완벽한 정답은 아니지만 그나마 중간 이상을 가는 모델은 1차원, 2차원 그래프인 것 같습니다. 이런 overfitting을 예방하기 위해서 우리는 그래프의 기울기 베타에 페널티를 주면 됩니다.
Regularization Method
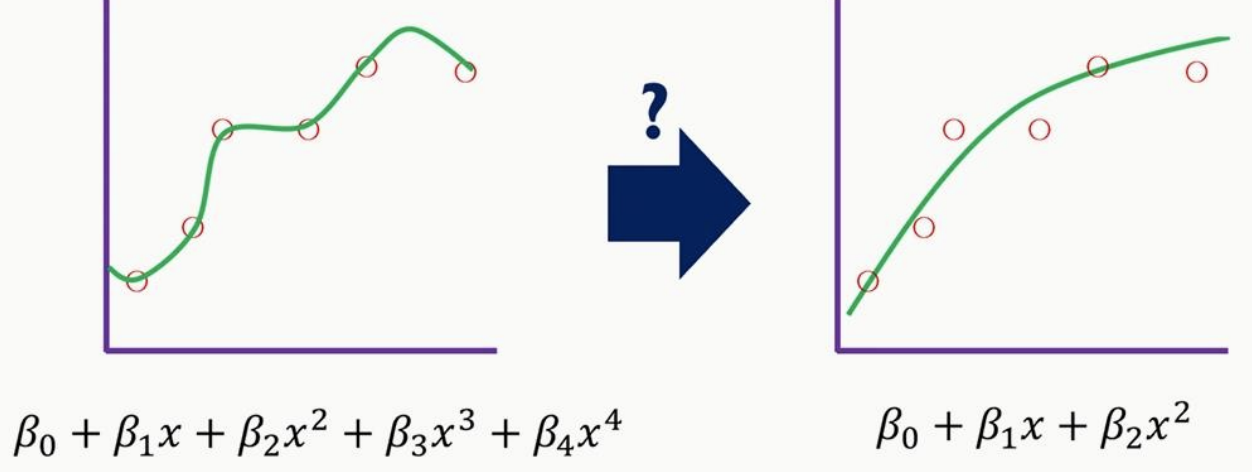
위 그림처럼 4차원 그래프가 존재하고 이 overfitting 된 그래프에 대한 min error를 구하는 식은 아래와 같습니다.
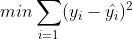
이때 만약에 베타(3, 4)에 예를들어 터무니없이 높은 값을 부여하면 min error를 구하기 위해 모델은 큰 값을 가진 베타(3,4)를 0으로 만들어버리게 됩니다. 그러면 위 오른쪽 그림처럼 training data에 약간의 error를 가지고 있어도 test data에 쓸 수 있는 cost function이 만들어집니다.

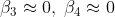
이런 overfitting을 예방하기위해 original cost function을 아래와 같이 바꿔줍니다.

이때, 람다는 error에 직접적으로 영향을 끼치기 때문에 가장 좋은 결과를 만들어내기위해 프로그래머가 적절하게 만들어줘야합니다. (이를 우리는 흔히 hyper parameter라고 부릅니다.)
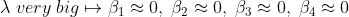
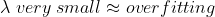
이처럼 정규화(Regularization) 컨셉을 처음으로 도입한 모델이 바로 Ridge Regression입니다.
Ridge Regression
릿지 회귀란 평균 제곱 오차를 최소화시키면서 회귀계수 β의 L2 norm을 제한하는 기법입니다. 릿지 회귀식을 공식화하면 아래와 같이 표현할 수 있습니다. 릿지 회귀식을 보면 잔자제곱항 + 페널티 항의 합으로 이루어져 있습니다. 람다가 크면 클수록 릿지 회귀식의 계수(베타) 추정식은 0에 가까워집니다.
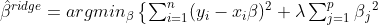
릿지 회귀식에는 제약조건이 있는데, 예를들어 optimal 한 회귀계수 β(1,2)를 찾아야하는게 우리의 목표라면

위 표를 기준으로 MSE가 제일 작은 (4, 5) 베타가 최소입니다. 일반 선형 회귀 모델이었다면, (4, 5)가 일반 회귀 계수로 결정되었을 겁니다. 하지만, 여기에 (β_1)^2 + (β_2)^2 이 합이 30 이하여야한다는 제약조건을 가해봅시다. 그러면 표에 상단 세가지는 고려에서 제외됩니다. 나머지 세 가지 중에 가장 MSE가 작은 (2,4)가 회귀 계수로 고려되는 것이 릿지 회귀의 방식입니다.
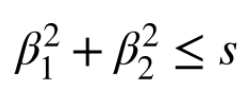
기하학적으로 조금 더 접근을 해보면 MSE (평균제곱오차) 식을 표현하면 아래와 같이 전개할 수 있습니다.

이때, MSE 식은 원추곡선을 그리게 되는데
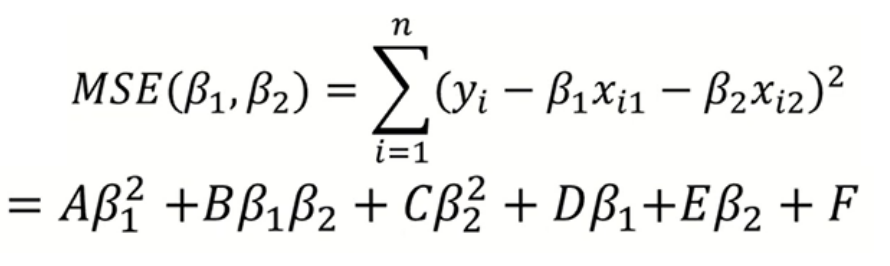
아래와 같이 판별식을 계산해서 풀어보면 0보다 작다고 합니다. 판별식이 0보다 작을 때 타원의 형태가 된다고 하여 아래 MSE의 형태는 타원의 형태를 이루게 됩니다.

아래의 MSE 타원이 점차적으로 커지는 모습을 볼 수 있는데 이는 회귀계수 β(1,2)를 점차적으로 증가시키면서 제약조건에 맞는 회귀계수 β를 찾는 과정입니다.

우리가 찾아야할 Error를 최소화시키는 MSE와 제약조건 베타(1,2)의 원 영역에 들어오는 파란색 부분이 Overfitting을 예방한 optimal 한 회귀계수 β(1, 2) 입니다. 다음으로 알아볼 방법은 릿지 회귀와 같이 자주 등장하는 방법인데 라쏘 회귀라고 합니다.
Lasso Regression
라쏘 회귀식은 아래와 같습니다. 모양은 릿지회귀와 매우 흡사하지만 빨간 네모칸의 제곱 식이 아니라 절댓값으로 바뀐 게 큰 차이점입니다.

랏쏘 회귀식은 릿지와는 다르게 해를 단박에 구 할 수 없습니다. 이때문에 다양한 방법들이 제안되었는데, MSE의 형태는 동일하게 타원인 반면 아래와 같이 제약조건이 원의 형태가 아닌 절댓값의 형태이기에 마름모의 모습을 띄게 됩니다.


이런 마름모의 모양은 예측에 중요하지않는 변수들의 회귀계수를 감소시킴으로써 변수선택에 효과적이라고 합니다. 릿지와 라쏘의 성능 표를 만들면 아래와 같이 구성됩니다.
| 구분 | 릿지회귀 | 라쏘회귀 |
| 제약식 | 𝐿2 norm | 𝐿1 norm |
| 변수선택 | 불가능 | 가능 |
| solution | closed form | 명시해 없음 |
| 장점 | 변수간 상관계수가 높아도 좋은 성능 | 변수간 상관계수가 높으면 성능↓ |
| 단점 | 크기가 큰 변수를 우선적으로 줄임 | 비중요 변수를 우선적으로 줄임 |
지금까지 연속형 데이터에 따른 Regression에 대해 알아보았고 Training data에 적절한 cost function을 만들고 Training data에 대한 overfitting을 예방하기 위해 Regularization Method 방법 두 가지 릿지와 라쏘에 대해 알아보았습니다.
본 글은 Hanyang University Computer and Software - Dong-Kyu Chae 교수님 수업 자료를 바탕으로 구성하였습니다.
Reference
https://ratsgo.github.io/machine%20learning/2017/05/22/RLR/
https://nittaku.tistory.com/284
https://deepinsight.tistory.com/135
https://ellun.tistory.com/106
https://medium.com/nerd-for-tech/linear-regression-icebreaker-to-machine-learning-algorithms-b5f680d19d4d
'Machine learning' 카테고리의 다른 글
| Gradient Descent (0) | 2021.09.25 |
|---|---|
| Random Forest (0) | 2021.09.20 |
| Decision Tree (0) | 2021.09.19 |
| correlation coefficient (피어슨 상관계수) (0) | 2021.08.24 |
| covariance matrix (공분산 행렬) (0) | 2021.08.21 |