Support Vector Machine(SVM)

What is SVM?

SVM은 기계 학습의 분야 중 하나로 패턴 인식, 자료 분석을 위한 지도 학습 모델이며, 주로 분류와 회귀 분석을 위해 사용한다. 두 카테고리 중 어느 하나에 속한 데이터의 집합이 주어졌을 때, SVM 알고리즘은 주어진 데이터 집합을 바탕으로 하여 새로운 데이터가 어느 카테고리에 속할지 판단하는 비확률적 이진 선형 분류 모델을 만든다. 

-위키백과, 우리 모두의 백과사전(서포터 벡터 머신)

 

간단하게 서포터 벡터 머신은

어떻게 공간상에서 optimal 한 decision boundaries를 찾는가?

입니다. 아래 그림을 보시면 두 개의 집단이 있고 그 집단을 가장 잘 분류할 수 있는 Linear discriminant function을 만들어야 합니다. 하지만 두 개의 집단을 나누는 직선을 만들다 보니 굉장히 많은데 우리는 이 중에 가장 optimal 한 Linear discriminant function(아래 그림에서는 직선)을 찾아야 합니다. 그 방법으로 서포터 벡터 머신이라는 알고리즘을 사용해 찾아보도록 하겠습니다. 

 

 

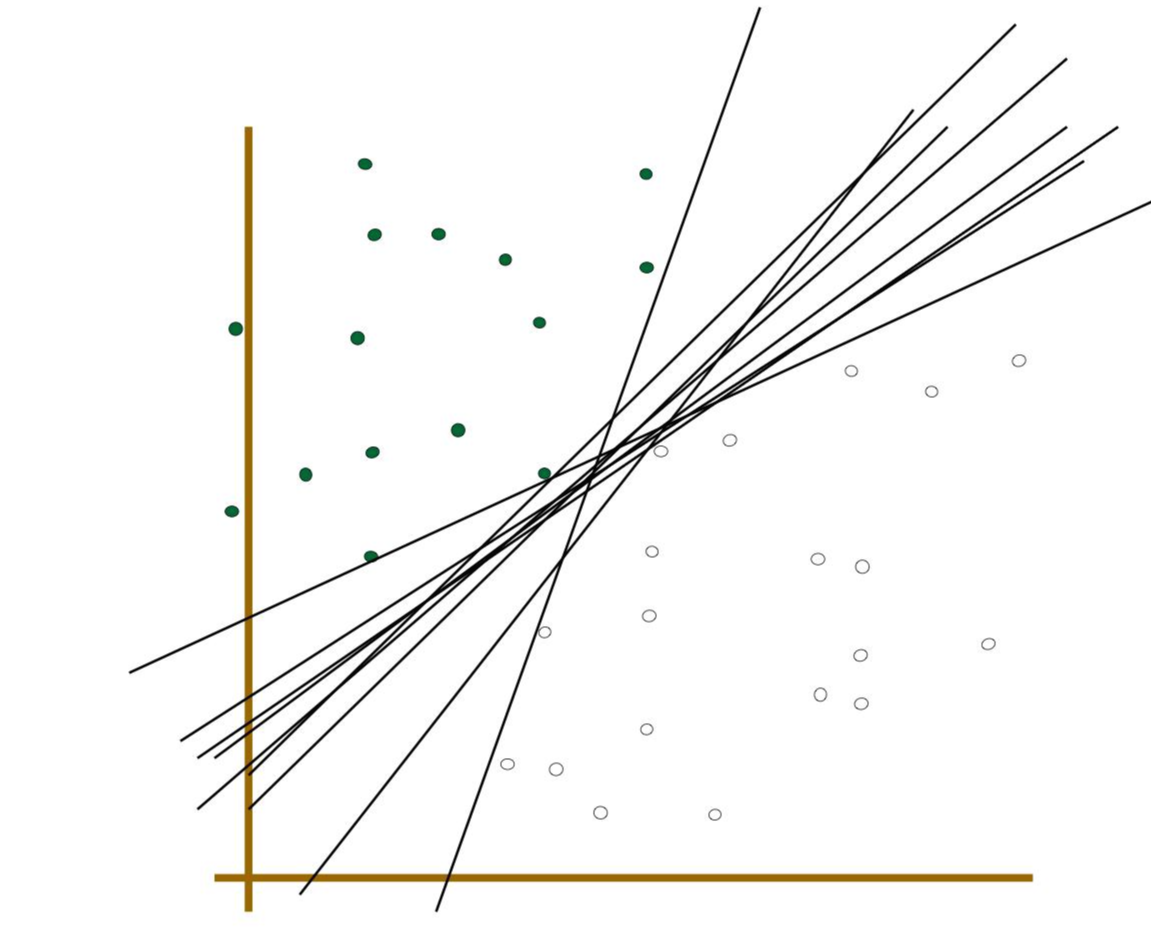
SVM의 철학은 Margin이라는 놈을 Maximize 하는 것입니다. 그렇다면 이 Margin이라는 놈이 뭔지에 대해 먼저 알아보겠습니다.

---

Margin

Margin은 각각의 class들의 decision boundary로의 거리입니다. 하지만 각각의 class의 기준점을 어디로 둬야 decision boundary의 거리를 알 수 있는데, class의 중심을 잡기에는 너무 추상적입니다. 먼저 어떤 class의 기준점을 잡는지 보겠습니다.

 

아래의 그림을 보시면 두 개의 class(x1, x2)를 잘 분류할 수 있는 H1과 H2라는 직선이 있습니다. 이때 이 직선들과 가장 인접한 각 class의 data가 곧 기준점이 되고 이 기준점을 support vector라고 부릅니다. 각각의 class들의 decision boundary로부터의 margin을 알 수 있습니다. 하지만 H1과 H2의 margin을 대충 비교해도 H2의 margin이 더 큰 값임을 알 수 있습니다. 우리의 서포터 벡터는 Margin이라는 놈을 Maximize 해야 하니 큰 값을 가진 H2 직선을 골라야겠지요. 

 

 

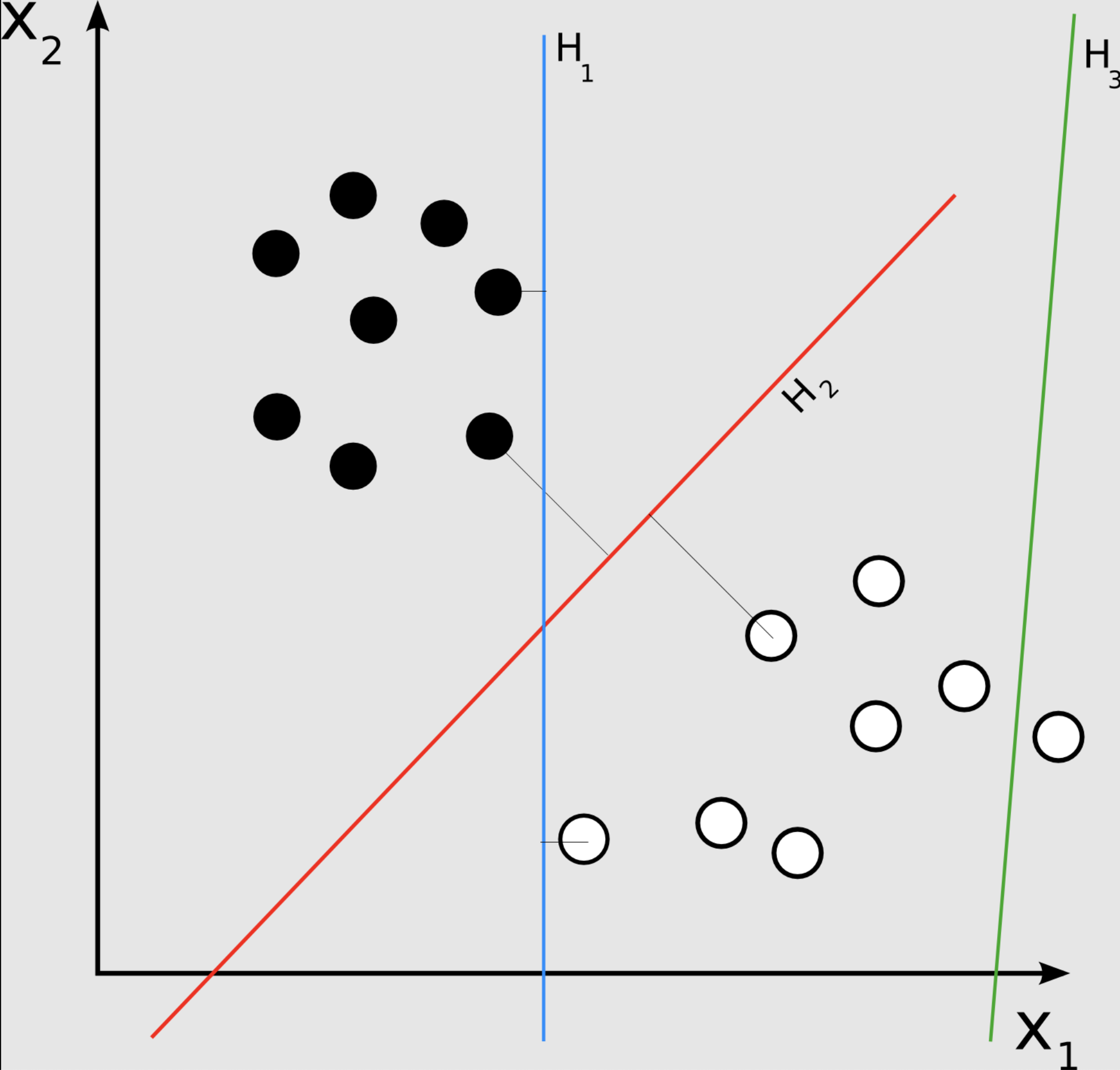
Why Maximize margin?

그렇다면 왜 항상 최댓값을 가지는 Margin을 찾아야 할까요? margin은 hyperplane과 each class 사이의 거리를 의미합니다. 너무 학습 데이터에 오버 핏팅을 방지하기 위해 일부러 일정한 크기를 노이즈로 집어넣어 일반화 오류(Generalization error)를 줄이면서 데이터의 판별 정확도를 높이기 때문입니다.  그러면 trining data뿐만 아니라 test data에서도 어느 정도의 성능은 보장이 됩니다.

 

---

Margin 구하는 방법

Maximize margin을 찾기 전에 먼저 margin을 구하는 방법에 대해 알아보겠습니다. 다음 그림을 보면 

 

 

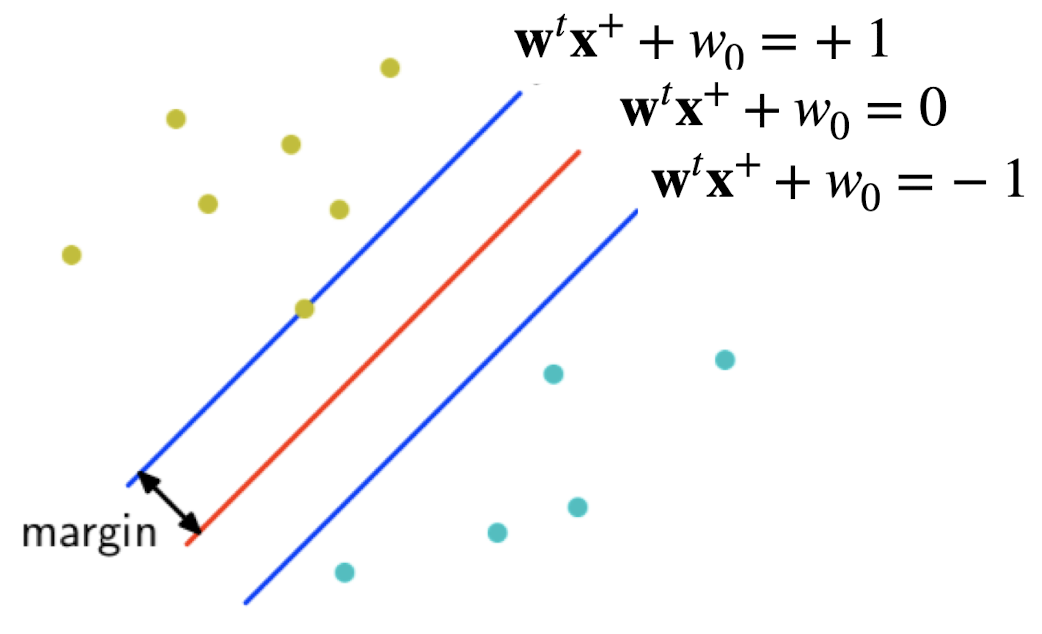
SVM은

Decision boundary

 

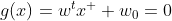
이라는 Unique 한 Decision boundary를 찾은 후에 x에 데이터들을 넣어 양수, 음수에 따라 class를 분류합니다. 그렇다면 우리는 이제 g(x)의 법선(직교) 벡터를 활용하여 Margin을 구할 수 있습니다. 아래 그림에서 d가 margin이고 직선 g(x)에서 x로의 마진을 구해보겠습니다.

 

 

 

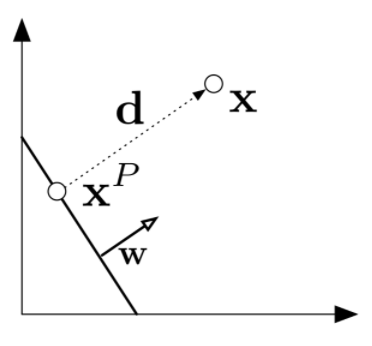
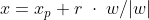
x도 g(x)와 동일한 방향의 직선을 그리면 아래와 같이 구할 수 있는데 이를 통하여 g(x)에 대입하여 풀면 margin을 구할 수 있습니다.

 

 

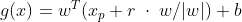
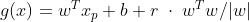
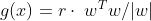
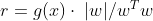
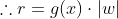
그렇다면 이제 Maximize margin을 찾아야 합니다. 이때, 라그랑지 함수(Lagrange Multiplier)가 사용됩니다.

 

라그랑지 함수(Lagrange Multiplier)

라그랑지란, 어떤 함수가 제약식 조건을 만족하면서 해당 '어떤 함수'가 갖는 최댓값 또는 최솟값을 찾고자 할 때 사용되는 함수이다.

 

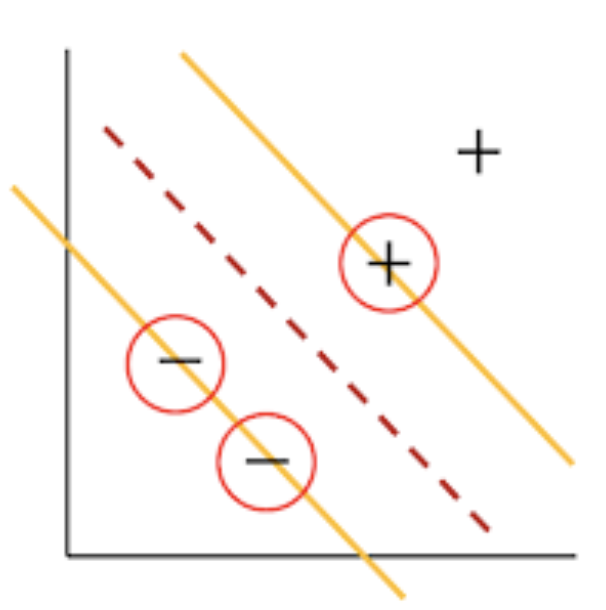
다시 한번 우리의 목표는 어떻게 공간상에서 optimal 한 decision boundaries를 찾는가? 입니다. 여기서 optimal한 decision boundaries는 곧 Maximize margin을 찾는 것이고 이는 곳 아래 그림처럼 '+'와 '-' class 사이 간의 거리를 최대한 넓게 하는 게 요지입니다.  

 

+와 - class 간의 거리를 구하는 법

 

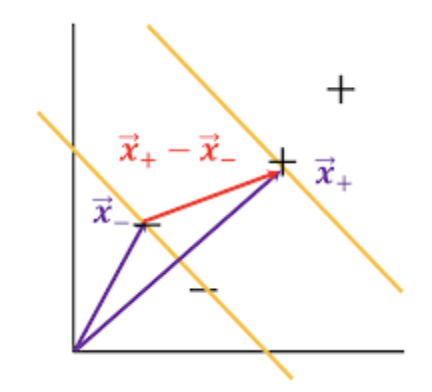
 위 그림을 보시면 결국 x_와 x+까지의 거리는 다음과 같이 표시할 수 있습니다.

 

 

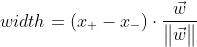
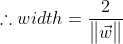
우리는 위 식에서 width를 최대화시켜주기 위해서 w를 최소화를 시켜야 하는 문제를 풀어야 합니다. 

 

 

이 최소화 문제를 풀기 위해 라그랑지 함수를 사용하면 아래와 같은 식을 풀어야 하는데

 

Lagrange Multiplier Method 라그랑지 승수법

 

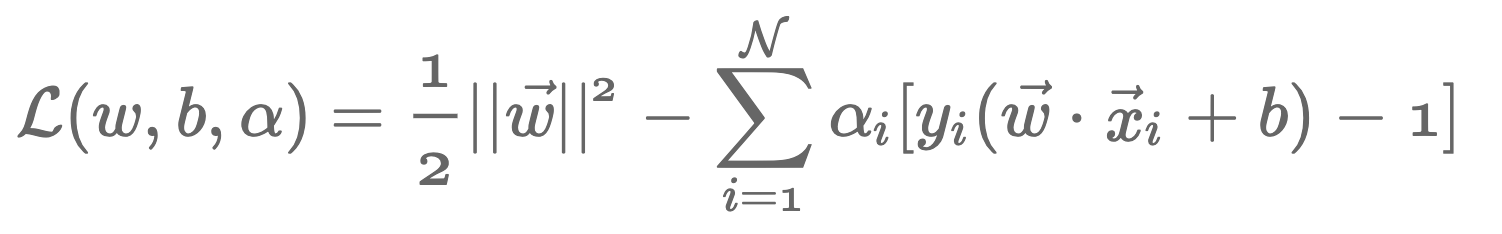
여기서 알파의 계수를 크게 해 주면 우리가 풀고자 하는 최소화 문제를 풀 수 있습니다.

 

 

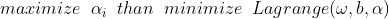
알파의 계수를 크게 만들어주려면 먼저 라그랑주 L에 대해 오메가와 b를 미분해주면 식이 아래와 같이 각각 변함을 알 수 있습니다.

 

 

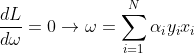
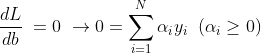
이제 최적화된 오메가와 b를 원래 함수 라그랑주 함수에 대입을 해줍니다. 이때 우리는 KKT Condition을 고려해야 합니다. 

 

 

---

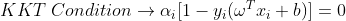
KKT Condition이란, α가 0인지 아닌지에 따라 나뉩니다. KKT 조건에서 알파 값이 0이 아니고 조건식이 1이면 x_i는 서포터 벡터

 

 

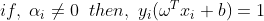
조건식이 1이 아니고, 알파 값이 0이면 x_i는 서포터 벡터가 아닌 값

 

---

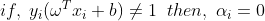
자 이제 오메가와 b를 원래 함수 라그랑주 함수에 대입을 해줍니다. 그렇다면 식을 단순화를 시킬 수 있는데, 기존 라그랑주 함수 식에서 두 번째 항(시그마)에서 -1 부분을 밖으로 빼주고 b에 대한 미분식을 집어넣으면 b 부분을 없앨 수 있습니다. 이어서 오메가에 대한 미분식을 집어넣으면 아래와 같이 정리할 수 있습니다.

 

 

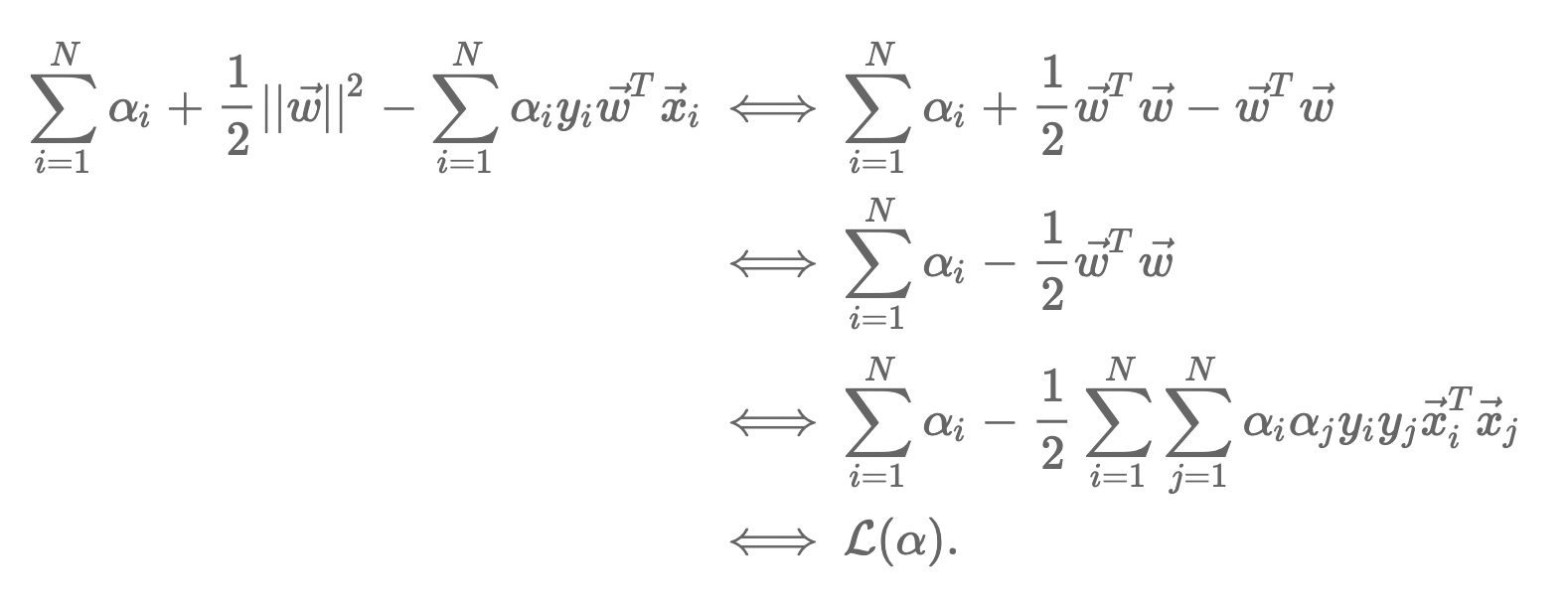
이제 알파에 대한 maximization 문제를 정의했습니다. 위 식을 풀어 α를 구하게 되면 위 두 개의 미분식(오메가, b)식에서 오메가와 비도 구할 수 있습니다. 그렇다면 이제 KKT Condition에 조건에 맞는 알파 값을 구하면 서포터 벡터를 알 수 있습니다.

 

빨간색 원은 서포터 벡터

 

라그랑주 함수 식을 찬찬히 살펴보면 α에 대해 첫째 항은 선형이고 둘째 항은 quadratic 형태이기 때문에 quadratic programming을 사용하면 어떤 알고리즘이든 α에 대한 해를 구할 수 있습니다.

 

즉, 신경망과 달리 SVM은 local minima에 빠질 걱정이 없습니다. 서포터 벡터들로 정해진 decision boundary는 가장 최적화 boundary이며 현재 가지고 있는 데이터들만으로 새로운 데이터들이 들어왔을 때 일반화를 가장 잘 시킨다고 합니다.

 

 

 

Reference

https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote09.html 

https://techblog-history-younghunjo1.tistory.com/78      

http://jaejunyoo.blogspot.com/2018/01/support-vector-machine-1.html