벡터란, 크기와 방향을 나타내는 물리량이다.
그렇다면 이 글에서 소개하는 직교 벡터(Orthogonal vector)란, 두 벡터가 수직(직교) 한다라는 말과 같다.
(직교 벡터는 2차원이 아닌, 모든 n 차원에 대해서 해당한다.)
예를 들어 아래 그림 1과 같이 $ x $ 와 $ y $ 처럼 두 벡터가 2차원 상에 존재한다.
빨간색 벡터인 $ x $는 x축 방향으로 뻗어있고, 파란색 벡터인 $ y $는 y축 방향으로 뻗어있다.
이 두 벡터가 이루는 각도는 서로 직각이며, 두 벡터를 더했을 때 초록색 벡터인 $ c $가 만들어진다.
초록색 벡터와 빨간색 벡터를 가만히 보면 피타고라스의 직각삼각형이 만들어진다.
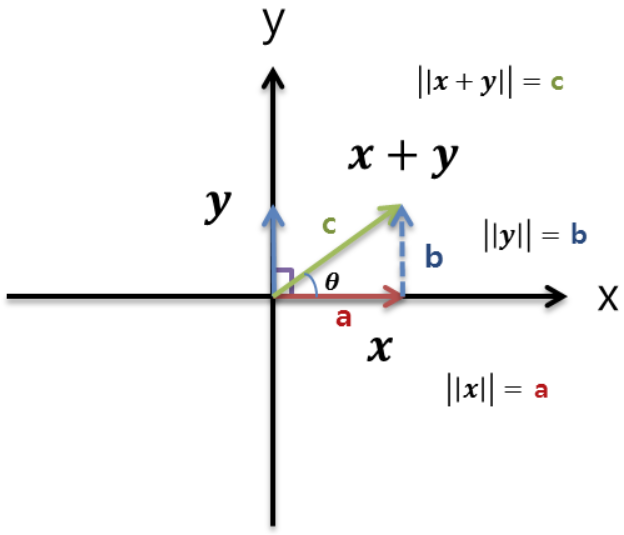
2차원 벡터로 구성되어있을때는 우리는 위 그림처럼 쉽게 그림을 그리면서 설명할 수 있다.
하지만 2차원을 넘어 3차원 4차원으로 넘어갈수록 표현 자체가 어려워진다.
그러면 우리는 두 벡터가 직교인지 아닌지를 판단하려면 2차원으로만 표현해야하는가?
이론적으로 두 벡터가 직교인지 아닌지를 내적(dot product)를 통해 알 수 있다.
중고등학교 때 배웠던 내적에 대한 식 (1)은 아래와 같다.
$$ Dot \ product:\boldsymbol{a} \cdot \boldsymbol{b}=
\left\| \boldsymbol{a}\right\| \cdot \left\|\boldsymbol{b} \right\|cos\theta \cdots (1) $$
대학교 때 선형대수학에서 다뤘던 내적은 아래와 같이 식 (2)로 표현 하기도 했다.

식 (1)에서 $ ||a|| $, $ ||b|| $는 각각의 벡터의 크기(norm)를 나타낸다.두 벡터 사이의 각도에 대한 cosine이 들어가 있는데 이 cosine 때문에 두 벡터가 직교(orthogonal)할 경우 그 결과 값이 0이 나오는 것이다. 내적을 dot 연산자와 함께 추상적으로 표현한 식 (1)을 실제적으론 식 (2)와 같이 row vector와 column vector의 곱으로 표현한다.
$ x $의 $ transpose $가 붙은 이유는 보통 벡터는 $ x, y, v $와 같이 하나의 볼드체(Bold) 문자로 표기하는데 일반적으로 볼드체로 표현되는 벡터들은 column vector를 나타낸다. 그런데 이를 row vector로 만들지 않으면 곱셈 자체를 할 수 없다. 벡터나 행렬의 곱셈연산을 하기 위해선 가령 [1x3]과 [3x1]과 같이 중간의 차원이 맞아야 곱셈이 가능한데, 그냥 colum vector 두 개는 [3x1], [3x1]처럼 가운데 차원이 맞지 않다. 따라서 row와 column의 곱셈으로 만들어줘야 하기 때문에 (2)와 같이 $ transpose $를 해주는 것이다. 이렇게 row와 column vector의 곱셈을 해주면 각 벡터의 같은 요소들끼리 곱하여 더해주는 연산을 하게 된다.
그렇다면 왜 내적을 해서 0이 되면 두 벡터가 직교일까?
피타고라스 정리로부터 그 이유를 찾아보자.
위 그림 1에 나타나있는 두 벡터와 삼각형을 식으로 표현하면 아래 식 (3) 같이 표현이 가능하다.
$$ \left\| \textbf{x} \right\|^2+\left\|\textbf{y} \right\|^2=\left\| \textbf{x+y}\right\|^2 $$
중학교때는 단순히 $ x $의 제곱 $ y $의 제곱, 그리고 대각선은 $ c $등의 문자로 배웠지만 여기서는 약간 표현 방법이 다르다. 벡터로 표현했기 때문이다. 즉, 벡터 $ x $의 크기의 제곱과 $ y $의 크기의 제곱은 삼각형의 대각선 $ x+y $의 크기의 제곱과 같다는 말이다.
식(3)을 더 구체적인 예시로 3차원 벡터로 계산을 해보자.
$$ \textbf{x}=\begin{bmatrix}
2 \\ 1
\\ 3
\end{bmatrix},
\textbf{y}=\begin{bmatrix}
3 \\ 3
\\ -3
\end{bmatrix} $$

위의 식은 오로지 직각 삼각형의 형태처럼 직교(orthogonal)하는 벡터들 사이에서만 성립하는 것이고, 피타고라스 정리와 연관지어 설명하기 위해 만들어진 예시이다. $ y $에 직교하지 않는 다른 벡터를 넣으면 식이 틀리는 것을 알 수 있다.
위 3차원 벡터 예시처럼 $|| x ||$는 벡터 $ x $의 크기, 즉 벡터의 길이(length)를 의미한다. 이것을 norm이라고 부르는데, norm에도 L2-norm, L1-norm등 다양한 방식이 존재한다. norm에 대해서는 다음에 정리를 해보자.일반적으로는 L2-norm을 나타내고 그것이 위 식에 나타낸 것이다. 가만히 보면 L2-norm을 구하는데 있어 식 (3)과 비슷한 패턴이 보일 것이다. 이는 어떤 임의의 벡터 크기를 계산하는 원리가 피타고라스의 정리로부터 나온 것이기 때문이다.
그림 1처럼 $ x + y $ 벡터의 크기는 벡터의 각 요소의 제곱을 더해 제곱근를 씌운 것과 같다. 이 방법은 n차원의 벡터에 모두 동일하게 적용된다.
위 예시를 좀 더 선형대수적인 방법으로 표현해보자. 그렇다면 아래와 같이 식 (4)로 표현할 수 있다.
$$ \textbf{x}^T\textbf{x}+\textbf{y}^T\textbf{y}=(\textbf{x}+\textbf{y})^T (\textbf{x}+\textbf{y}) $$
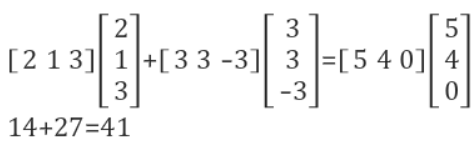
식 (4)에 있는 벡터를 가지고 실제로 계산해보니 답이 같은 것을 알 수 있다. 이를 통해 식 (3)을 우리가 기존에 알던 식 (4)의 방식과 벡터 방식으로 표현한 (5)가 같다는 것을 이해할 수 있다.
그렇다면 식 (1) ~ (4)에 걸쳐 설명한 피타고라스의 직각삼각형에 대한 정리가 내적(dot product)와 어떤식으로 연결된다는 건가?
식 (4)를 풀어서 정리하면 알 수 있다.
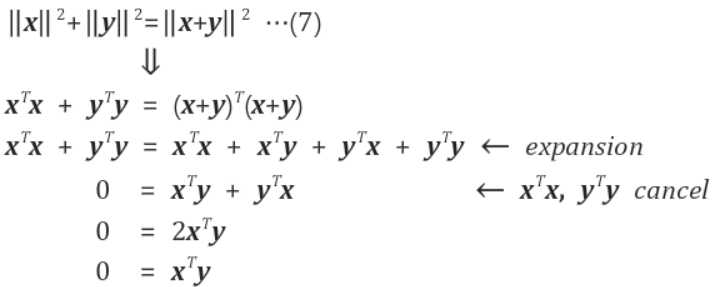
먼저 우변에 있는 식을 전개한다. 이때 좌변과 우변에 $ x^T x$ $ y^T y$가 각각 존재하므로 소거할 수 있다.
이들을 소거하면 좌변에 동일한 $ x^T x$ $ y^T y$를 소거할 수 있고 0이 된다.
그러면 우변에는 $ x^T y$ $ y^T x$가 남는데, $a*b$나 $b*a$나 어차피 똑같기 때문에 같은 것으로 간주할 수 있다.
따라서 $2x^Ty$가 되고 2는 상수이기 때문에 무시할 수 있다. 이렇게 피타고라스의 직각삼각형에 대한 정리로부터 내적(dot product)를 유도하였다. 결론적으로 차원이 동일한 두 벡터를 내적하였을 때 그 결과값이 0이면 두 벡터는 직교(orthogonal)하며 두 벡터 사이의 각도는 90도이다.
만약 $a$ 벡터와 $b$벡터를 내적하는데 $b$가 영벡터(zero vector)라면?
이 두 벡터는 직교(orthogonal)일까? 영벡터인 벡터와 내적하는 모든 벡터는 서로 직교를 하기 때문에 직교이다.
왜냐하면 직교에 대한 정의 자체가 내적했을 때 결과가 0인 것으로 되어 있기 때문이다.
해당 게시글은 순순히 공부 차원에서 작성한 글입니다.
REFERENCE
'Linear Algebra' 카테고리의 다른 글
| 고유값과 고유벡터(eigenvalue & eigenvector) (0) | 2023.11.04 |
|---|